Kruskal Algorithm이란?
탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것
- 탐욕적인 방법
- 결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 것
- 탐욕적인 방법은 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증해야 한다.
- 다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다.
- MST 가 1) 최소 비용의 간선으로 구성됨 2) 사이클을 포함하지 않음 의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택 한다.
Kruskal Algorithm의 동작
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
- 사이클을 형성하는 간선을 제외한다.
- 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
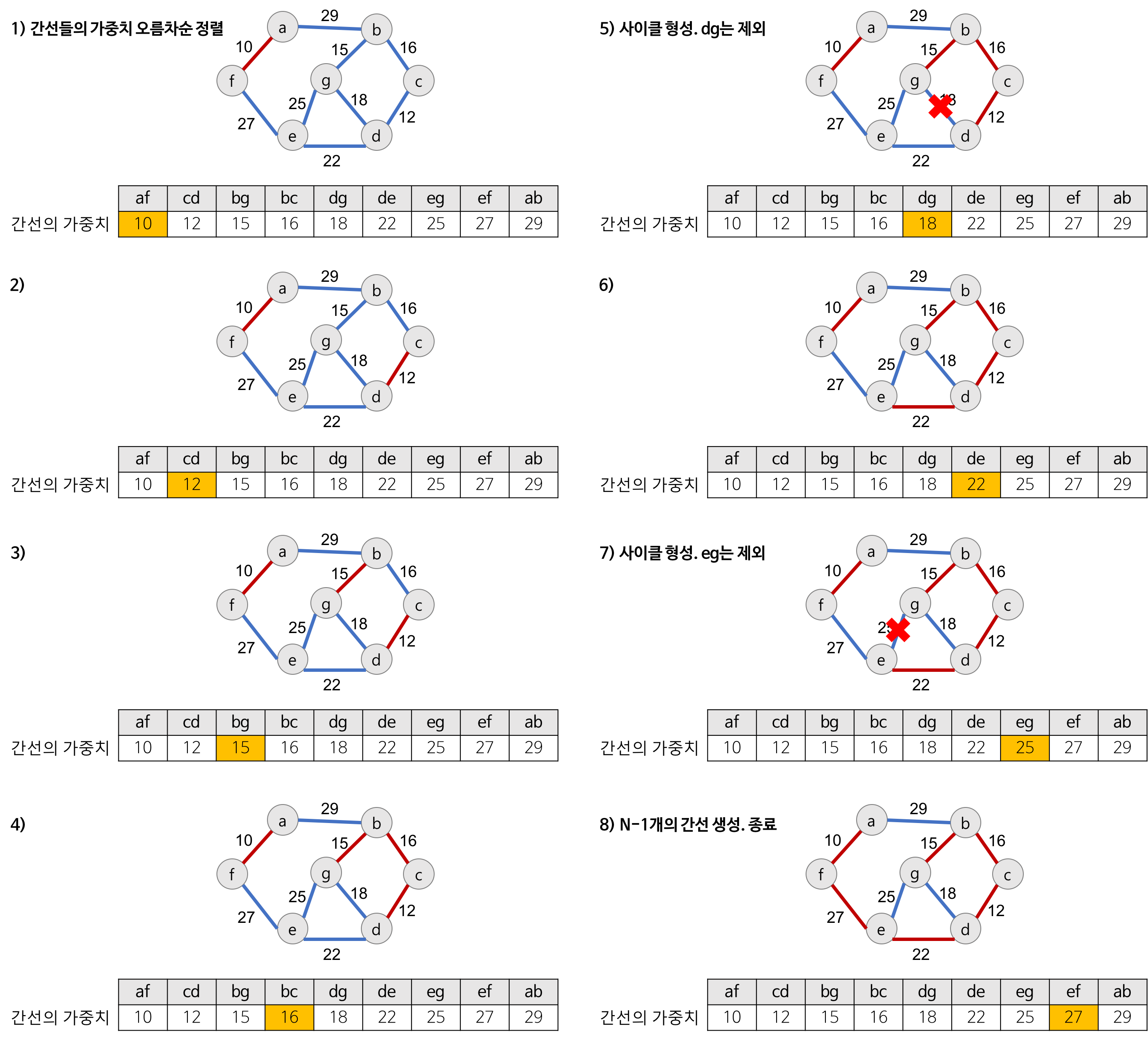
Kruskal Algorithm의 구체적인 동작 과정
Kruskal 알고리즘을 이용하여 MST(최소 비용 신장 트리)를 만드는 과정
- 간선 선택을 기반 으로 하는 알고리즘
- 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
주의!
- 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지를 체크!
- 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결할 때 사이클이 형성된다.
- 즉, 추가할 새로운 간선의 양끝 정점이 같은 집합에 속해 있으면 사이클이 형성된다.
- 사이클 생성 여부를 확인하는 방법
- 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지를 먼저 검사해야 한다.
- ‘union-find 알고리즘’ 이용
Kruskal Algorithm 구현
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct edge {
int src, dest, weight;
bool operator <(const edge& rhs) const {
return weight < rhs.weight;
}
};// 간선 정보
vector<edge> vt;
int parent[10001];
int v, e, k;
int find(int);
bool merge(int, int);
int main() {
scanf("%d %d", &v, &e);
for (int i=1; i<=v; i++) {
parent[i] = i;
}// 자기 자신을 부모로 초기화
edge tmp;
for (int i=0; i<e; i++) {
scanf("%d %d %d", &tmp.src, &tmp.dest, &tmp.weight);
vt.push_back(tmp);
}
sort(vt.begin(), vt.end());// 가중치 오름차순 정렬
for (int i=0; i<e; i++) {
if (merge(vt[i].src, vt[i].dest)) {
k += vt[i].weight;// 최적의 가중치를 더한다
}// 사이클 없이 합칠 수 있으면 합친다
}
printf("%d\n", k);
return 0;
}
int find(int u) {
if (u == parent[u]) return u;
return parent[u] = find(parent[u]);
}
bool merge(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return false;// 사이클 방지
parent[v] = u;
return true;
}Kruskal Algorithm의 시간 복잡도
- union-find 알고리즘을 이용하면 Kruskal 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우된다.
- 즉, 간선 e개를 퀵 정렬과 같은 효율적인 알고리즘으로 정렬한다면
- Kruskal 알고리즘의 시간 복잡도는 O(elog₂e) 이 된다.
- Prim의 알고리즘의 시간 복잡도는 O(n^2) 이므로
- 그래프 내에 적은 숫자의 간선만을 가지는 ‘희소 그래프(Sparse Graph)’의 경우 Kruskal 알고리즘이 적합하고
- 그래프에 간선이 많이 존재하는 ‘밀집 그래프(Dense Graph)’ 의 경우는 Prim 알고리즘이 적합하다.
출처: https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html
'Algorithms' 카테고리의 다른 글
| 진수변환에 대해서 (0) | 2020.07.01 |
|---|---|
| Algorithm - Prim Algorithm (0) | 2020.06.19 |
| Algorithm - 최소 신장 트리(MST, Minimum Spanning Tree) (1) | 2020.06.17 |
| Algorithms - Merge Sort (합병정렬) (1) | 2020.03.05 |
| Algorithms - Quick Sort (퀵정렬) (1) | 2020.03.05 |