정렬 알고리즘 중에서도 비효율적인 방법중 하나라고 할 수는 있지만, 간단하게 구현할 수 있는 알고리즘 중 하나입니다. 선택정렬은 간단하게 이동하면서 작은 수(또는 큰 수)가 발견될때마다 위치를 바꿔주는 것을 말합니다~
코드
#include <iostream>
using namespace std;
int main(){
int idx;
int temp;
int arr[7]={1,9,4,10,85,12,46};
for(int i=0;i<sizeof(arr)/sizeof(int);i++){
int min =998765;
for(int j=i;j<sizeof(arr)/sizeof(int);j++){
if(min>arr[j]){
min = arr[j];
idx=j;
}
}
temp = arr[i];
arr[i] = arr[idx];
arr[idx] = temp;
}
for(int i=0;i<sizeof(arr)/sizeof(int);i++){
cout<<arr[i];
}
return 0;
}선택 정렬(selection sort) 알고리즘 개념 요약
- 제자리 정렬(in-place sorting) 알고리즘의 하나
- 입력 배열(정렬되지 않은 값들) 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
- 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
- 첫 번째 순서에는 첫 번째 위치에 가장 최솟값을 넣는다.
- 두 번째 순서에는 두 번째 위치에 남은 값 중에서의 최솟값을 넣는다.
- …
- 과정 설명
- 주어진 배열 중에서 최솟값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교체한다(패스(pass)).
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
- 하나의 원소만 남을 때까지 위의 1~3 과정을 반복한다.
선택 정렬(selection sort) 알고리즘의 구체적인 개념
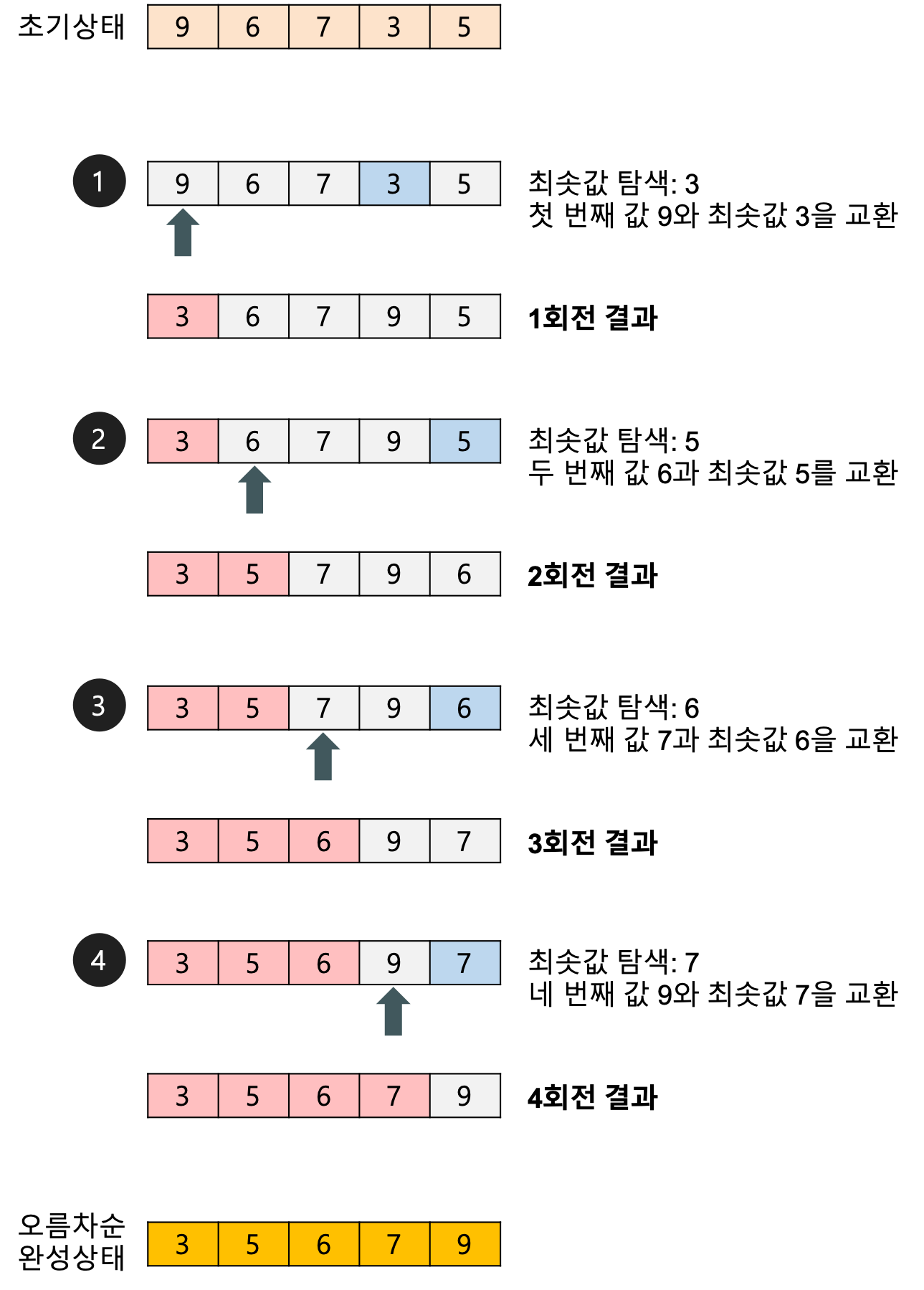
- 선택 정렬은 첫 번째 자료를 두 번째 자료부터 마지막 자료까지 차례대로 비교하여 가장 작은 값을 찾아 첫 번째에 놓고, 두 번째 자료를 세 번째 자료부터 마지막 자료까지와 차례대로 비교하여 그 중 가장 작은 값을 찾아 두 번째 위치에 놓는 과정을 반복하며 정렬을 수행한다.
- 1회전을 수행하고 나면 가장 작은 값의 자료가 맨 앞에 오게 되므로 그 다음 회전에서는 두 번째 자료를 가지고 비교한다. 마찬가지로 3회전에서는 세 번째 자료를 정렬한다.
그림설명
선택 정렬(selection sort) 알고리즘의 특징 및 시간복잡도
- 장점 : 자료 이동 횟수가 미리 결정된다.
- 단점 : 안정성을 만족하지 않는다. 즉, 값이 같은 레코드가 있는 경우에 상대적인 위치가 변경될 수 있다.
시간 복잡도 계산
- 비교 횟수
- 두 개의 for 루프의 실행 횟수
- 외부 루프: (n-1)번
- 내부 루프(최솟값 찾기): n-1, n-2, … , 2, 1 번
- 교환 횟수
- 외부 루프의 실행 횟수와 동일. 즉, 상수 시간 작업
- 한 번 교환하기 위하여 3번의 이동(SWAP 함수의 작업)이 필요하므로 3(n-1)번
- T(n) = (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)

- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
출처: https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html
'Algorithms' 카테고리의 다른 글
| Algorithm - 최소 신장 트리(MST, Minimum Spanning Tree) (1) | 2020.06.17 |
|---|---|
| Algorithms - Merge Sort (합병정렬) (1) | 2020.03.05 |
| Algorithms - Quick Sort (퀵정렬) (1) | 2020.03.05 |
| Algorithms - Bubble Sort (버블정렬) (0) | 2020.03.05 |
| Algorithms - Insertion Sort (삽입정렬) (0) | 2020.03.04 |