https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10) 입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다. 방향은 0, 1, 2,
www.acmicpc.net
문제 설명
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
☛ 1. 시작 점 2. 시작 방향 3. 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.
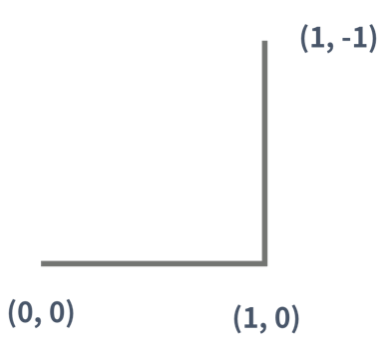
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)
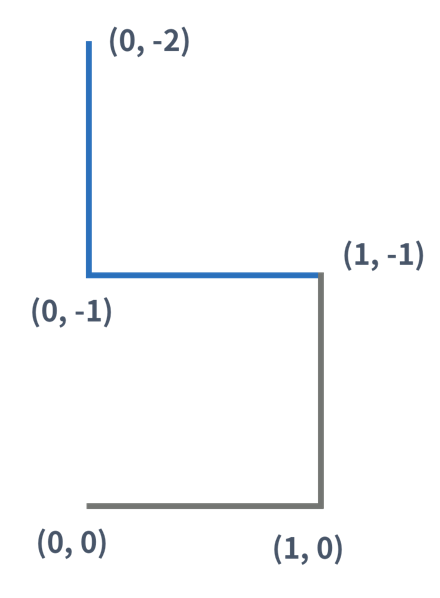
3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.

크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다.
x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
접근 방법
☛ 0: x좌표가 증가하는 방향 (→)
☛ 1: y좌표가 감소하는 방향 (↑)
☛ 2: x좌표가 감소하는 방향 (←)
☛ 3: y좌표가 증가하는 방향 (↓)
문제를 보고 평행이동과 회전변환이 떠올라서 이 두 개를 활용해 문제를 풀었습니다. 어려운 문제는 아니지만 좌표이동이 좀 까다로울 수 있다고 생각합니다.
DIRECTION
1. x, y, d, g를 받는다. (단 x, y를 받을 때 바꿔서 받아야 합니다.)
2. g가 0일때부터 n일 때까지의 Dragon Curve를 만들어간다.
2-1. 단 g가 0일때에는 하나만 추가한다.
2-2. 나머지 경우에는 마지막 생성된 점을 기준으로 처음 생성된 점까지 (평행이동 ➤ 회전변환 ➤ 평행이동)을 진행한다.
(저는 2-2 코드를 그래도 복사에서 활용했지만 심플하고 간결한 코드를 원하시면 공통의 Function을 만드는 것을 추천드립니다. 저는 게을러서 ㅠㅠ..)
3. 사각형의 개수를 구하기 위해서 사각형의 모든 점이 Dragon Curve에 포함되어 있는 개수를 합산합니다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
int n,y,x,d,g,ans=0;
bool map[101][101];
// 0: x좌표가 증가하는 방향 (→)
// 1: y좌표가 감소하는 방향 (↑)
// 2: x좌표가 감소하는 방향 (←)
// 3: y좌표가 증가하는 방향 (↓)
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
vector<pair<int,int> >dragon_curve[n];
memset(map,false,sizeof(map));
//n번 반복
for(int i=0;i<n;i++){
cin>>x>>y>>d>>g;
dragon_curve[i].push_back(make_pair(y,x));
//세대만큼 회전을 스택으로 쌓으면서 반복
for(int j=0;j<=g;j++){
if(d==0){
if(j==0){
dragon_curve[i].push_back(make_pair(y,x+1));
}
else{
int Size = dragon_curve[i].size();
int pinofY = dragon_curve[i][Size-1].first;
int pinofX = dragon_curve[i][Size-1].second;
for(int k=Size-2;k>=0;k--){
int movePinY = dragon_curve[i][k].first-pinofY;
int movePinX = dragon_curve[i][k].second-pinofX;
int resultPinY = movePinY*0 + movePinX*(1) + pinofY;
int resultPinX = movePinY*(-1) + movePinX*0 + pinofX;
dragon_curve[i].push_back(make_pair(resultPinY,resultPinX));
}
}
}
else if(d==1){
if(j==0){
dragon_curve[i].push_back(make_pair(y-1,x));
}
else{
int Size = dragon_curve[i].size();
int pinofY = dragon_curve[i][Size-1].first;
int pinofX = dragon_curve[i][Size-1].second;
for(int k=Size-2;k>=0;k--){
int movePinY = dragon_curve[i][k].first-pinofY;
int movePinX = dragon_curve[i][k].second-pinofX;
int resultPinY = movePinY*0 + movePinX*(1) + pinofY;
int resultPinX = movePinY*(-1) + movePinX*0 + pinofX;
dragon_curve[i].push_back(make_pair(resultPinY,resultPinX));
}
}
}
else if(d==2){
if(j==0){
dragon_curve[i].push_back(make_pair(y,x-1));
}
else{
int Size = dragon_curve[i].size();
int pinofY = dragon_curve[i][Size-1].first;
int pinofX = dragon_curve[i][Size-1].second;
for(int k=Size-2;k>=0;k--){
int movePinY = dragon_curve[i][k].first-pinofY;
int movePinX = dragon_curve[i][k].second-pinofX;
int resultPinY = movePinY*0 + movePinX*(1) + pinofY;
int resultPinX = movePinY*(-1) + movePinX*0 + pinofX;
dragon_curve[i].push_back(make_pair(resultPinY,resultPinX));
}
}
}
else{
if(j==0){
dragon_curve[i].push_back(make_pair(y+1,x));
}
else{
int Size = dragon_curve[i].size();
int pinofY = dragon_curve[i][Size-1].first;
int pinofX = dragon_curve[i][Size-1].second;
for(int k=Size-2;k>=0;k--){
int movePinY = dragon_curve[i][k].first-pinofY;
int movePinX = dragon_curve[i][k].second-pinofX;
int resultPinY = movePinY*0 + movePinX*(1) + pinofY;
int resultPinX = movePinY*(-1) + movePinX*0 + pinofX;
dragon_curve[i].push_back(make_pair(resultPinY,resultPinX));
}
}
}
}
}
for(int i=0;i<n;i++){
for(int j=0;j<dragon_curve[i].size();j++){
map[dragon_curve[i][j].first][dragon_curve[i][j].second]=true;
}
}
for(int i=0;i<100;i++){
for(int j=0;j<100;j++){
if(map[i][j]&&map[i][j+1]&&map[i+1][j]&&map[i+1][j+1]) ans++;
}
}
cout<<ans<<"\n";
return 0;
}funny algorithm 0.0
'Algorithms > BOJ' 카테고리의 다른 글
| 백준 17142 - 연구소 (0) | 2020.05.08 |
|---|---|
| 백준 17140 - 이차원 배열과 연산 (0) | 2020.05.07 |
| 백준 17779 - 게리맨더링2 (0) | 2020.05.05 |
| 백준 15683 - 감시 (0) | 2020.05.01 |
| 백준 14891 - 톱니바퀴 (0) | 2020.04.30 |
